论钢塔架及钢筋砼混合结构自振周期的取值
关键词:混合结构;振型;自振周期
建(构)筑物的自振周期是建(构)筑物按某一振型完成一次自由振动所需的时间,由结构自身的形式、质量、刚度决定,是建(构)筑物主要的动力特征。《建筑结构荷载规范》(GB50009-2001)7.4.1条规定对于高度大于30m且高宽比大于1.5的房屋和基本自振周期大于0.25s的各种高耸结构以及大跨度屋盖结构,均应考虑风压脉动对结构发生顺风向风振的影响。风振计算应按随机振动理论进行,结构的自振应按结构动力学计算。以7.4.2条为例:;其中ξ为脉动增大系数,其值除与基本风压有关外,直接受结构自振周期的影响,详见《建筑结构荷载规范》表7.4.3及条文说明。对于复杂的高层钢结构和钢筋混凝土混合结构,在实际的设计工作中,自振周期有不同的取法,这里我们对不同的计算方式得到的周期进行讨论。
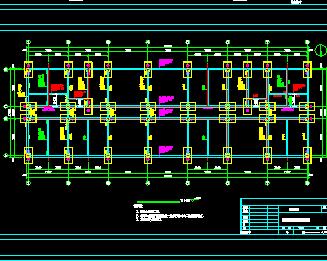
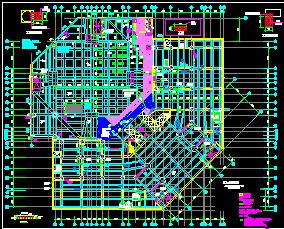
本文以石化行业某塔框架为例讨论混合结构自振周期的取用问题。某化工塔框架为下部两层钢筋混凝土框架(0m~18.1m),共六柱(1.8mx1.8m),第一层平台顶标高11.5m,第二层平台顶标高18.1m;18.1m以上为多层钢结构平台(标高18.1m~55.0m为等尺寸矩形钢平台,标高55.0m~100.0m为尺寸逐渐变小的钢塔架),塔(30m左右高,壁厚30mm,直径9m)底部位于标高为18.1m钢筋混凝土平台上,塔与平台采用螺栓连接。简图见模型1及模型2
1规范法
根据《建筑结构荷载规范》(GB50009-2001)附录E结构基本自振周期的经验
公式中E.1.2具体结构中2石油化工塔架中第二项框架基础塔(塔壁厚不大于30mm)
T1=0.56+0.40×10-3H2/D0(E.1.2.3)
计算钢筋砼框架及塔的自振周期T1tT1t=0.56+0.40×10-3×55.22/9=0.695
根据E.2.1中1钢结构T1=(0.1~0.15)×n(n为层数)(E.2.1.1)
计算钢结构部分的自振周期T1sT1s=(0.1~0.15)×19=1.9~2.89
规范(经验)法分别对混凝土框架和钢结构计算自振周期,难以体现组合结构的振动特性。
2空间计算法1:塔简化为质点
在staadpro中建模,钢筋混凝土框架、钢结构塔架均建入,塔简化为位于塔重心高度处的质点,和钢筋混凝土框架以主从节点方式发生关系,通过staadpro地震工况(LOADCASE10)下结构振动的分析后得出不同的振型及相应的周期,根据各振型振动情况及参与质量的分析确定针对钢筋混凝土框架及塔部分和钢结构部分的周期,具体分析如下:
2.1模型1
2.2各振型周期表
2.4典型振型图
2.5周期取用分析,根据比较振型1、2、9、14为控制振型
振型1,由振动动态图可知主要振动为钢结构Z向,钢筋混凝土框架及塔的位移振幅较小,钢结构部分振幅较大,参与质量X向为0,Z向为14.06,参与质量与钢结构部分自重所占的比重接近,故选用此周期作为钢结构Z向计算风荷载用,T=2.67s
振型2,由振动动态图可知主要振动为钢结构X向,钢筋混凝土框架及塔的位移振幅较小,钢结构部分振幅较大,参与质量X向为10.43,Z向为0,参与质量与钢结构部分自重所占的比重接近,故选用此周期作为钢结构X向计算风荷载用,T=2.40s
振型9由振动动态图可知主要振动为钢筋混凝土结构Z向,钢筋混凝土框架及塔的位移振幅较大,参与质量X向为0,Z向为70.55,参与质量与钢筋混凝土框架及塔部分自重所占的比重接近,且塔位于钢筋混凝土框架上,振动应是同一的,故选用此周期作为塔及钢筋混凝土框架结构Z向计算风荷载用,T=1.30s
振型14由振动动态图可知主要振动为钢筋混凝土结构X向,钢筋混凝土框架及塔的位移振幅较大,参与质量X向为46.1,Z向为0.07,参与质量与钢筋混凝土框架及塔部分自重所占的比重接近,且塔位于钢筋混凝土框架上,振动应是同一的,且塔与钢筋混凝土刚接,振动应是同一的,故选用此周期作为塔及钢筋混凝土框架结构Z向计算风荷载用,T=1.20s
3空间计算法1:塔按实际刚度建模
在staadpro中建模,钢筋混凝土框架、钢结构塔架均建入,塔按照一个杆件建入,杆件截面形式按照同设备壁厚高度钢管建入,塔的自重及操作介质重以构件均布荷载的形式输入,风荷载计算后输在与钢筋混凝土平台连接的节点上,此节点和钢筋混凝土框架以主从结点方式发生关系,通过staadpro地震工况(LOADCASE10)下结构振动的分析后得出不同的振型及相应的周期,根据各振型振动情况及参与质量的分析确定针对钢筋混凝土框架及塔部分和钢结构部分的周期,具体分析如下:
3.1模型2
3.2各振型周期表
由于输入杆件较多,60种振型后达到参与质量大于95%
3.4典型振型图
3.5周期取用分析根据比较振型1、2、9、14为控制振型
振型1由振动动态图可知主要振动为钢结构Z向,钢筋混凝土框架及塔的位移振幅较小,钢结构部分振幅较大,参与质量X向为0,Z向为14.58,参与质量与钢结构部分自重所占的比重接近,故选用此周期作为钢结构Z向计算风荷载用,T=2.68s
振型2由振动动态图可知主要振动为钢结构X向,钢筋混凝土框架及塔的位移振幅较小,钢结构部分振幅较大,参与质量X向为10.67,Z向为0,参与质量与钢结构部分自重所占的比重接近,故选用此周期作为钢结构X向计算风荷载用,T=2.40s
振型9由振动动态图可知主要振动为钢筋混凝土结构Z向,钢筋混凝土框架及塔的位移振幅较大,参与质量X向为0,Z向为47.82,参与质量与钢筋混凝土框架及塔部分自重所占的比重接近,且塔位于钢筋混凝土框架上,振动应是同一的,故选用此周期作为塔及钢筋混凝土框架结构Z向计算风荷载用,T=1.55
振型14由振动动态图可知主要振动为钢筋混凝土结构X向,钢筋混凝土框架及塔的位移振幅较大,参与质量X向为69.06,Z向为0.04,参与质量与钢筋混凝土框架及塔部分自重所占的比重接近,且塔位于钢筋混凝土框架上,振动应是同一的,且塔与钢筋混凝土刚接,振动应是同一的,故选用此周期作为塔及钢筋混凝土框架结构Z向计算风荷载用,T=1.43s
4根据上述结果比较可以得出
4.1规范公式与建模比较可得钢结构部分差异不大,但钢筋混凝土框架及塔部分相差较大,原因可能有一下两条:
4.1.1建模中并未考虑混凝土框架及塔上的管道同周边管架、管道等的拉结作用所以周期偏大,实际使用时应于调整。
4.1.2建模中对11.5m及18.1m的钢筋混凝土楼板简化为梁格,对刚度有一定影响。但如果既建楼板又建梁会使刚度偏大,因此为安全计算,仍采用梁格布置。
4.2两种建模方式结果的差异性主要源于塔型设备的简化,按照模型1,以质点的形式输入由于刚度无穷大所以周期比模型2按照钢杆件输入的要略小,实际应用中,考虑到设备壁厚是变化的,按照钢杆件输入可以较为真实的模拟塔型设备的刚度。
4.3规范中(E.1.2.3)的公式不适应于塔壁厚大于30mm的各类设备塔架的基本自振周期计算,通过模型2这种方法可以根据模拟的钢杆件壁厚改变来模拟此类塔型设备。